domingo, 9 de enero de 2011

El Pendulo de Foucalt

Close

Péndulo de Foucault

 
Para la novela de Umberto Eco, véase El péndulo de Foucault.
Animación del péndulo de Foucault

Un péndulo de Foucault es un péndulo esférico que puede oscilar libremente en cualquier plano vertical y capaz de oscilar durante mucho tiempo (horas). Se utiliza para demostrar la rotación de la Tierra y el efecto Coriolis. Se llama así en honor de su inventor, León Foucault.

 

[editar] Descripción y fundamento

Esquema de un dispositivo para ilustrar el fundamento del péndulo de Foucault
Péndulo de Foucault en el Polo Norte. El péndulo oscila en un plano constante en el espacio, mientras que la Tierra gira por debajo de él.
Movimiento de rotación de la Tierra debajo del péndulo de Foucault

Consideremos en primer lugar el dispositivo que mostramos en la Figura. Si hacemos girar la plataforma mientras el péndulo está oscilando, observaremos que el plano de las oscilaciones permanece inalterado con respecto a un observador inercial. Este efecto se debe a la inercia de la masa pendular. Puesto que las dos fuerzas que actúan sobre ella (su peso y la tensión del hilo) están contenidas en el plano de las oscilaciones, éstas, una vez iniciadas, tendrán lugar siempre en un mismo plano. Para cambiar el plano de las oscilaciones se requeriría una componente de fuerza normal a dicho plano.

Por el contrario, resulta obvio que el plano de las oscilaciones no permanecerá inalterado para un observador situado sobre la plataforma giratoria, que será, evidentemente, un observador no inercial; para este observador, el plano de las oscilaciones efectuará una precesión alrededor del eje vertical (eje de rotación) en sentido contrario al de giro de la plataforma y con la misma celeridad angular (de precesión).

Esta propiedad de la inalterabilidad del plano de las oscilaciones del péndulo fue utilizada por el físico francés Bernard León Foucault (1819-68) para comprobar el movimiento de rotación de la Tierra en torno a su eje y demostrar que la Tierra no constituye un referencial inercial. Foucault realizó públicamente su experiencia en 1851, bajo la cúpula del Panteón de París, utilizando una masa de 28 kg suspendida de un hilo de 70 m de longitud. El periodo de un péndulo de esa longitud es de unos 17 s. La suspensión del extremo superior del hilo permitía al péndulo oscilar con igual libertad en todas las direcciones. Alrededor del punto del suelo que estaba directamente debajo del punto de suspensión se dispuso una balsa circular, llena de arena, de unos 3 m de radio, de modo que una aguja metálica colocada en la parte inferior de la masa pendular barría la arena en cada oscilación. Se vio con toda claridad que, en oscilaciones sucesivas, el plano de oscilación del péndulo rotaba en el sentido de las agujas del reloj. En una hora el plano de oscilación del péndulo giraba unos 11°, y la circunferencia se completaba en algo más de 32 horas.

¿Por qué gira el plano de oscilación del péndulo? Es fácil comprender que, si la experiencia se hubiera realizado en el Polo Norte, resultaría evidente que el plano de oscilación del péndulo permanecería fijo en un referencial inercial, mientras que la Tierra giraría bajo el péndulo a razón de una vuelta cada 24 horas. Por el contrario, un observador situado "sobre" la Tierra vería girar el plano de oscilación del péndulo en sentido contrario al de la rotación terrestre, dando una vuelta cada 24 horas. La situación es muy diferente y mucho más difícil de analizar cuando abandonamos el Polo Norte y nos situamos en un lugar de la Tierra de latitud geográfica λ. Entonces, como ya hemos visto al describir la experiencia de Foucault, el tiempo empleado por el plano de oscilación del péndulo para girar 360° es mayor del necesario en el Polo.

Cálculos cuidadosos permiten relacionar la velocidad angular Ω de rotación del plano de las oscilaciones del péndulo con la velocidad angular ω de rotación de la Tierra:

(1) \Omega=\omega \sin{\lambda}' \,

donde (90°-λ′) es el ángulo formado por la vertical del lugar y el eje de rotación de la Tierra. La aceleración gravitatoria aparente g* tiene la dirección de la vertical del lugar y como g* sólo está ligeramente desviada con respecto a g (0°6', como máximo), el ángulo λ′ es muy aproximadamente igual a la latitud geográfica del lugar, esto es, λ≈λ′. Obviamente, el plano de oscilación del péndulo precesa en el referencial del laboratorio con una velocidad angular Ω dada por la expresión (1). En el hemisferio Norte la precesión tiene lugar en el sentido horario (mirando hacia abajo).

Podemos interpretar del modo siguiente el resultado expresado por (1):

en un lugar de la Tierra, de latitud λ, el suelo se comporta como una plataforma giratoria con una velocidad angular Ω = ωz = ω sen λ

(componente vertical de la velocidad angular de la Tierra) de modo que el movimiento de precesión del péndulo de Foucault es el que corresponde a esa velocidad angular. De este modo, el tiempo empleado por el plano de oscilación del péndulo en dar una vuelta completa es

(2) T=\frac{2\pi}{\omega\sin{\lambda}} = \frac{24}{\sin{\lambda}} \text{horas}

y el ángulo girado en una hora \theta\, es función de la latitud del lugar:

(3) \theta = 15^o \sin{\lambda} \,

La experiencia del péndulo de Foucault es una prueba efectiva de la rotación de la Tierra. Aún si la Tierra estuviese y hubiese estado siempre cubierta de nubes, la experiencia de Foucault nos permitiría demostrar que la Tierra está girando. Igualmente, este péndulo permite determinar la latitud del lugar sin recurrir a observaciones astronómicas.

[editar] Fase geométrica

Véase también: Fase geométrica
Transporte paralelo sobre la superficie de una esfera.

Se ha reinterpretado el péndulo de Foucault como caso particular de la universalidad del concepto conocido como fase geométrica,[1] que por otro lado se relaciona con el transporte paralelo, que se ilustra en la figura, y con el teorema de Gauss-Bonnet,[2] que relaciona la curvatura de una superficie con su característica de Euler.

En este sentido, es fundamental tener en cuenta que el periodo de rotación de la Tierra es mucho más largo que el periodo de oscilación del péndulo. En concreto, el cambio de dirección de la fuerza de la gravedad que experimenta el péndulo —en el sistema de referencia de la Tierra— es lo bastante lento como para satisfacer el teorema adiabático,[1] de forma que no hay un intercambio efectivo de energía entre las dos oscilaciones.

[editar] Péndulos de Foucault relevantes

Véase también: Listado de péndulos de Foucault en el mundo
Péndulo de Foucault en el Museo de Artes y Oficios de París; detalle de las clavijas en el suelo.

Existe un péndulo de Foucault en la gran sala de entrada del edificio de las Naciones Unidas en Nueva York, y es frecuente encontrarlo en los grandes Museos de Ciencias.

[editar] Panteón de París

Su importancia histórica radica en que con él se hizo la primera demostración, en 1851. El péndulo se fijó a la cúpula del Panteón de París; medía 67 m y llevaba una masa de 28 kg. Una vez lanzado, el péndulo oscilaba durante 6 h. El periodo es de 16,5 s; el péndulo se desviaba 11° por hora. Su ciclo de giro completo dura algo más de 32 horas. El 6 de abril de 2010,[3] , el cable del péndulo se rompió, causando un daño irreparable al péndulo y al suelo de mármol del famoso panteón.[4]

[editar] Véase también

[editar] Referencias

  1. ↑ a b J. J. Sakurai (1993). Modern Quantum Mechanics. pp. 479-480. ISBN 978-0201539295. 
  2. ↑ Jens von Bergmann and HsingChi von Bergmann (2007). «Foucault pendulum through basic geometry». Am. J. Phys. 75:  pp. 888–892. doi:10.1119/1.2757623. 
  3. ↑ Le pendule de Foucault perd la boule
  4. ↑ Foucault's pendulum is sent crashing to Earth

[editar] Bibliografía

  • Marion, Jerry B. (1996) (en español). Dinámica clásica de las partículas y sistemas. Barcelona: Ed. Reverté. ISBN 84-291-4094-8. 
  • Ortega, Manuel R. (1989-2006) (en español). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. 
  • Resnick,Robert & Krane, Kenneth S. (2001) (en inglés). Physics. New York: John Wiley & Sons. ISBN 0-471-32057-9. 
  • Serway, Raymond A.; Jewett, John W. (2004) (en inglés). Physics for Scientists and Engineers (6ª edición). Brooks/Cole. ISBN 0-534-40842-7. 
  • Tipler, Paul A. (2000) (en español). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3. 

[editar] Enlaces externos

Publicado por en

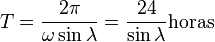
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)